![]()
GEOMETRIA SOLIDA - GLI ESAEDRI
IL CUBO
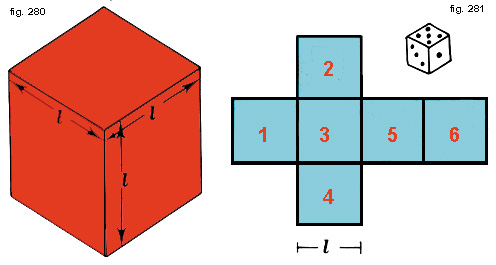
Sappiamo già che un esaedro è un poliedro con sei facce. Qui però ci occuperemo di alcuni esaedri particolarmente semplici che si incontrano spesso nella esperienza quotidiana. Il primo di questi è il cubo o esaedro regolare: le sue facce sono sei quadrati tutti uguali, il lato dei quali si chiama spigolo del cubo (fig. 280).AREA DELLA SUA SUPERFICIE
Ritagliando opportunamente la superficie lungo gli spigoli otteniamo lo sviluppo del cubo.Dalla fig. 281 deduciamo facilmente la seguente regola:
La superficie di un cubo equivale a sei volte la superficie di una sua faccia:
A = 6l2 (1)
VOLUME DEL CUBO
Osserviamo: un cubetto di lato 1 cm ha il volume di 1 cmc Per costruire un cubo di lato doppio occorrono 8 (cioè 23) cubetti e per costruirne uno di lato triplo ne occorrono 27 (cioè 33). Ne deduciamo che:Il volume del cubo è uguale alla terza potenza della misura del lato;
V = l3 (2)
IL PARALLELEPIPEDO RETTANGOLO
Il tuo libro di matematica, la tua stanza, il televisore, sono tutti oggetti che suggeriscono l'idea del parallelepipedo rettangolo. Diremo che:Il parallelepipedo rettangolo è un esaedro formato da sei facce rettangolari, a due a due uguali e parallele.
La lunghezza degli spigoli a, b, c, oppure a', b', c', o ancora a'', b'', c'', si dicono dimensioni rispettivamente del parallelepipedo, del televisore e del libro. La faccia su cui poggia il solido prende il nome di base (ad esempio il sottofondo del televisore e la copertina del libro).
![]()
![]()
AREA DELLA SUA SUPERFICIE
Anche il parallelepipedo può essere sviluppato come il cubo (fig. 284): si nota che le tre facce fra loro diverse hanno area ab, cb e ac, m poiché l'area totale è la somma delle aree delle sei facce. Si ha:A = 2ab + 2bc + 2ac (3)
VOLUME DEL PARALLELEPIPEDO
Osserva la fig. 285: lo spigolo AB è occupato da 2 cubetti, AC da 5 e AD da 3. Il parallelepipedo è formato da trenta cubetti, cioè esattamente 2¦3¦5. Se lo spigolo del cubetto misura un centimetro il volume totale sarà di 30 cmc. In generale possiamo dire che:Il volume del parallelepipedo è uguale al prodotto delle tre dimensioni:
V = a*b*c (4)
DIAGONALI
Osserviamo che il parallelepipedo e il cubo possiedono quattro diagonali uguali fra loro, che si incontrano tagliandosi a metà in un punto P. Calcoliamone la lunghezza. In virtù del teorema di Pitagora, possiamo scrivere:
+-------
CH² = DC²+DH² BH = \¦BC²+CH²
(5)
+----------- +----------
e quindi: BH = \¦BC²+DC²+DH² cioè d = \¦a²+ b²+ c²
La lunghezza della diagonale del parallelepipedo rettangolo è uguale alla radice
quadrata della somma dei quadrati delle tre dimensioni.Ricorda che il cubo si può considerare come un parallelepipedo rettangolo che ha le tre dimensioni tutte uguali; confronta infatti le formule (1) e (2) con le (3) e (4), che danno l'area e il volume rispettivamente del cubo e del parallelepipedo: la (3) diviene uguale alla (1) e la (4) diviene uguale alla (2) se si pone l al posto di a,b e c. Applicando lo stesso metodo con la (5) troveremo la diagonale del cubo:
+---------- +----
d = \¦l²+ l²+ l² = \¦3 l² = l ¹3 = l*1,732 (6)
PARALLELEPIPEDO OBLIQUO
Deformando un parallelepipedo rettangolo, alcuni o tutti i diedri non misureranno più 90°: saremo cioè in presenza di un parallelepipedo obliquo. Le sue facce saranno dei parallelogrammi a due a due uguali; deformando completamente un cubo le sue facce si trasformano in rombi e avremo un romboedro.![]()
![]()
VERO O FALSO?
1) Le diagonali di un parallelepipedo sono a due a due uguali.2) Il cubo è un parallelepipedo rettangolo con le tre dimensioni uguali.
3) Il parallelepipedo si dice rettangolo quando le sue facce sono dei rettangoli.
4) Il cubo è un esaedro regolare perché ha le facce e i diedri fra loro uguali.
5) Le diagonali di un romboedro non sono tutte uguali.
1) Falso: sono tutte e quattro uguali.
2) Vero.
3) Falso: si dice rettangolo se tutti i diedri sono uguali e quindi retti; infatti due delle sei facce possono anche essere quadrate.
4) Vero.
5) Vero.
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
ESERCIZI
(Sono già risolti ma tu prova a studiarli con l'aiuto della tav. 2)l) Calcolare l'area laterale di un parallelepipedo rettangolo di dimensioni cm 15, cm 20 e cm 37, considerando quest'ultima come altezza. Applicando la (3) si ha:
A l = cm2(15+20)*37 = cm2 2590
2) L'area totale di un parallelepipedo rettangolo misura m2 900. Determinare l'altezza sapendo che le dimensioni di base sono rispettivamente m 12 e m 15. Applicando la terza delle (4) inverse:
c = m[900-2(12+15)]:[2*(12+15)] = m 15,36
3) Calcolare il volume di un parallelepipedo rettangolo di dimensioni 9, 13 e 20. Applicando-la formula (S) si ha:
V = m3 9*13*20 = mc 2340
4) Calcolare l'area totale di un cubo di lato cm 8. Applicando la (9):
A t = cm2 (6*82) = cm2 384
5) Calcolare il volume di un cubo di lato cm 12. Applicando la (10):
V = cm3 123 = cm3 1728
6) Calcolare il lato di un cubo la cui diagonale misura m 24,248. Applicando la (11) inversa si ha:
l = m(24,248:1,732) = m 14
7) Un parallelepipedo obliquo è alto cm 25 e il parallelogrammo di base ha area di cmc 30. Calcolare il volume. Applichiamo la (7):
V = m3 (30*25) = m3 750
Affrontiamo ora un problema pratico.
Esempio. La pompa che alimenta la vasca di una piscina olimpionica è in grado
di erogare 25 litri d'acqua al secondo. La vasca, larga 25 metri e lunga 50, è
divisa in due zone di diversa profondità: la prima, destinata ai tuffi dal
trampolino, è profonda m 5 e si estende in lunghezza per 20 m, mentre la parte
restante è profonda solo m 2. Si chiede il tempo necessario al completo
riempimento della vasca.
Dobbiamo calcolare il volume della vasca e dividerlo poi per la portata (25
litri al secondo), ricordando che un litro corrisponde a 1 dmc. Osserviamo in
figura che la zona da riempire si compone di de parallelepipedi aventi in comune
la dimensione in larghezza di 25 m.
I) Calcoliamo il volume dell'acqua alta:
m3 (20*5*25) = m3 2500
II) Calcoliamo il volume dell'acqua bassa:
m3 (30*2*25) = m3 1500
III) Calcoliamo il volume totale e convertiamolo in litri:
V = m3 (2500+1500) = m3 4000 = litri 4.000.000
IV) Calcoliamo il tempo necessario al riempimento in secondi:
sec. (4.000.000:25) = sec. 160.000
Occorrono quindi 160.000 secondi, pari a 44 ore, 26 minuti e 40 secondi. In pratica, quasi due giorni.
Tabella riassuntiva degli esaedri
![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()